Quickhull Algorithm for Convex Hulls

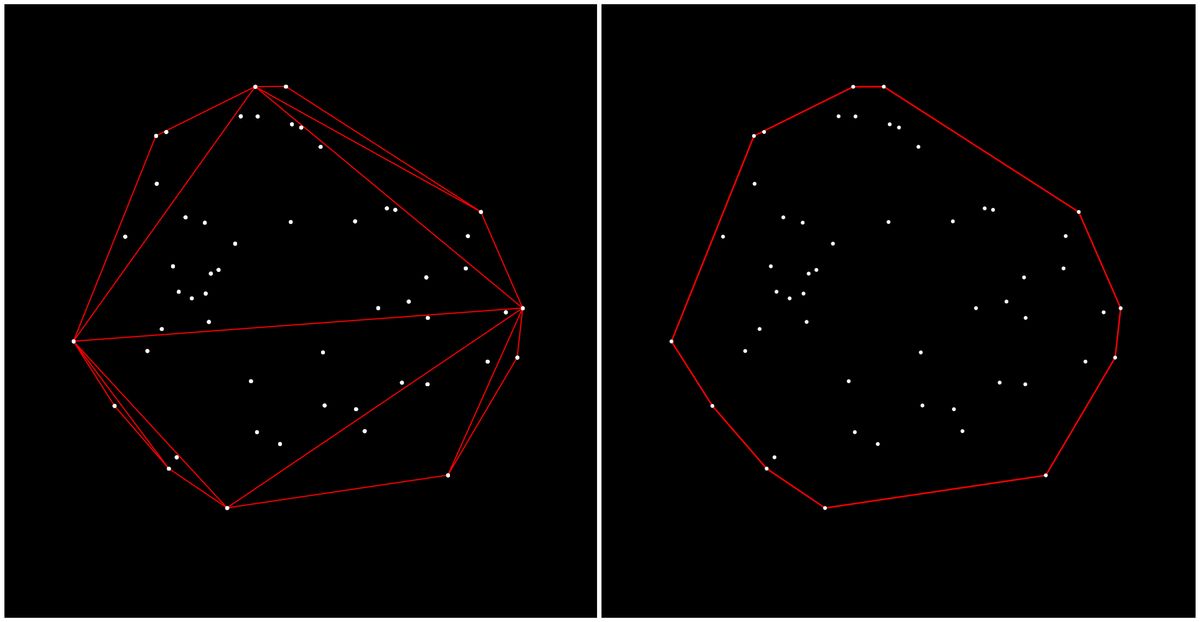
On Convex Hulls

Let's begin with the assumption that we have a set of points on a 2 dimensional plane. Now we'd like to roughly approximate the area that these points occupy and find the smallest possible convex polygon that encloses these points. How would we do this?

What actually is a convex polygon? Convex polygons are shapes that bulge outwards in every direction. Meaning that if you were to pick any two random points inside of such a shape, you would be able to draw a straight line that connects these two points, without having this line cross any of the shape's boundaries. Circles for example, are convex shapes, just like triangles, rectangles and really any regular polygon.

Concave shapes, on the other hand, are shapes that have at least one dent, where a straight line would end up crossing the boundaries of that shape. For instance, a crescent shape would be considered concave:

Convex hulls are super useful for solving a variety of different real life problems, generally because in many scenarios they have useful and advantageous properties. For instance, convex shapes are closed under intersection, meaning that the intersection of two convex shapes is in turn also always a convex shape. These properties make it super easy to compute certain operations on convex shapes (we will see an example later).

But let's get back to our example. In this manner, the convex hull is the smallest possible convex polygon that contains all of the points in the set. If the points in our set were tangible entities in the real world, we could simply find their convex hull by spanning a rubber band around them, such that it spans the outermost points of the set. But lest you want to implement an entire physics simulation to accomplish this approach, there's a number of established methods for this purpose.

In the next sections we'll have a close look at the inner workings of the Quickhull algorithm, that can be used to compute the convex hull of a set of points!

Quickhull Algo Pseudocode

Similarly to the Bowyer-Watson Triangulation Algo that we implemented last year, this time around we'll also start from a snippet of pseudo-code that can be found on Wikipedia. If you'd like to give it a shot, and try to implement the pseudo-code by yourself before reading on, now's your chance!

Otherwise give the following two functions a quick read 👇 the entire algo consists of two functions. The first of them is kind of a setup function that is required to get ball rolling:

Input = a set S of n points 
Assume that there are at least 2 points in the input set S of points

function QuickHull(_S_) is
    _// Find convex hull from the set S of n points_
    Convex Hull := {} 
    Find left and right most points, say A & B, and add A & B to convex hull 
    Segment AB divides the remaining (_n_ − 2) points into 2 groups _S1_ and _S2_ 
        where _S1_ are points in _S_ that are on the right side of the oriented line from _A_ to _B_, 
        and _S2_ are points in _S_ that are on the right side of the oriented line from _B_ to _A_ 
        
    FindHull(_S1_, _A_, _B_) 
    FindHull(_S2_, _B_, _A_) 
    
    Output := Convex Hull
end function

The second function, is the one that actually constructs the convex hull:

function FindHull(_Sk_, _P_, _Q_) is
    _// Find points on convex hull from the set Sk of points_ 
    _// that are on the right side of the oriented line from P to Q_
    **if** _Sk_ has no point **then**
        **return**
    From the given set of points in _Sk_, find farthest point, say _C_, from segment _PQ_ 
    Add point _C_ to convex hull at the location between _P_ and _Q_ 
    Three points _P_, _Q_, and _C_ partition the remaining points of _Sk_ into 3 subsets: _S0_, _S1_, and _S2_ 
        where _S0_ are points inside triangle PCQ, _S1_ are points on the right side of the oriented 
        line from _P_ to _C_, and _S2_ are points on the right side of the oriented line from _C_ to _Q_. 
    FindHull(_S1_, _P_, _C_) 
    FindHull(_S2_, _C_, _Q_) 
end function

If you noticed, there's a bit of an odd thing happening towards the end of the second function... it makes a call to it's own function signature?!

The Quickhull algorithm is recursive. Recursion in programming refers to a technique where a function calls itself to solve a problem. Recursion is usually used when a larger task can be split up into several smaller sub-tasks that mirror the problematic of the original task. Solving these smaller tasks ultimately culminates into solving the bigger overarching problem at hand.

Suppose you want to tidy up a messy room; to make this more manageable we could start by cleaning each corner individually before we move on to another. For each individual corner, you could then in turn start by clearing the elevated surfaces such as the shelves and desks first, then move on to surfaces closer to the ground. Equivalently, each surface can be split into smaller regions to clean and so on, until the task becomes small enough that it no longer makes sense to divide it further sub-tasks. That is roughly how recursion works.

This way of solving problems is also often referred to as the Divide and Conquer paradigm. Where we divide a problem into smaller tasks, conquer these smaller sub-tasks and then combine their solutions into a larger solution for the overall problem. The Quickhull algorithm is a recursive divide and conquer algorithm.

Algorithm Breakdown

Now that we've set the scene and covered the necessary related concepts, let's discuss the code a little bit more in detail.

The initialization steps in the first function:

1. Given a set of points S, we'll find the two points A and B, that have a minimum and maximum x coordinate among all points in the set. These two points are with certainty part of the convex hull, because they make up the horizontal extremities of the set.

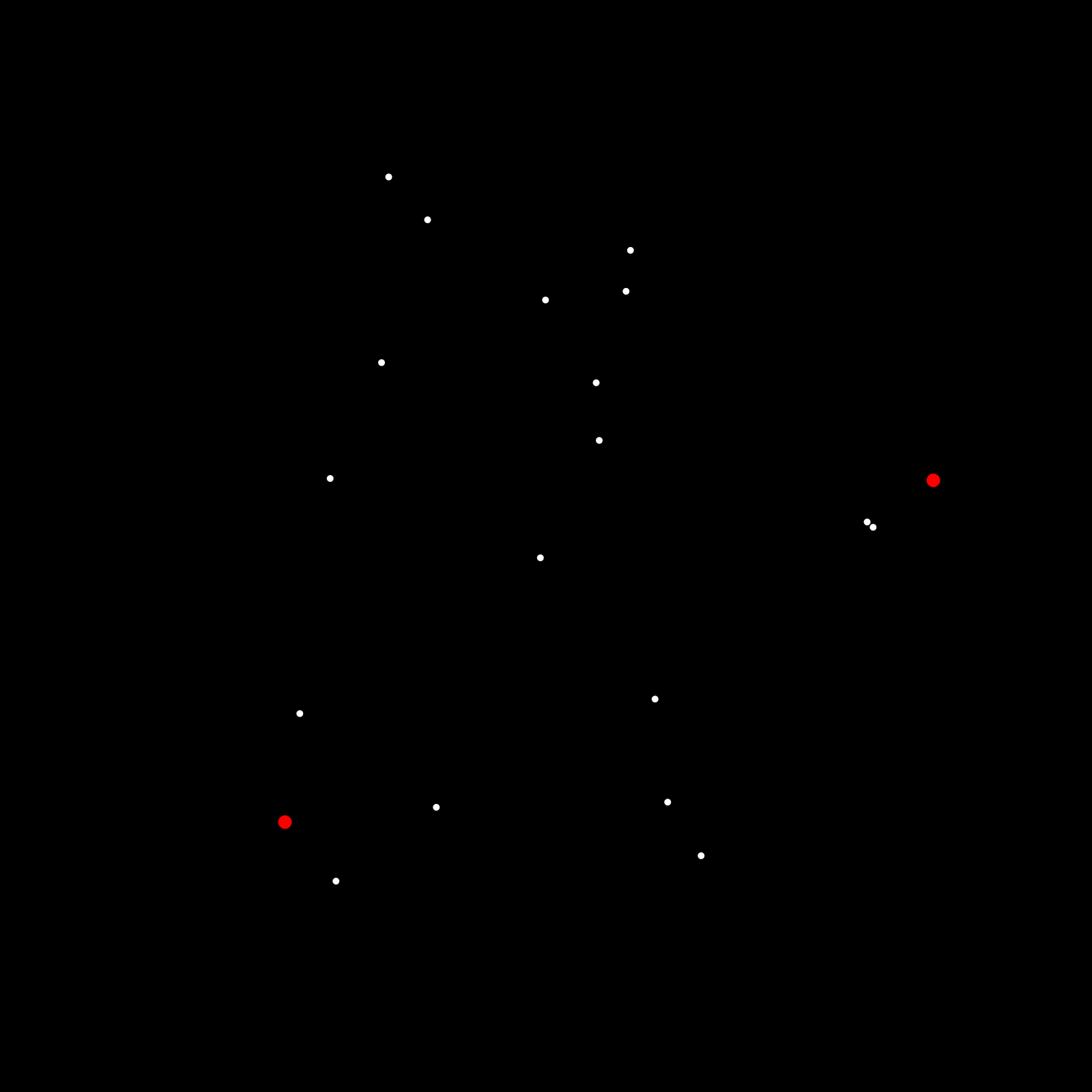
2. The line that connects these two extremities, splits the entire set of points into two halves. Here it's important to point out (pun not intended) that this line needs to be treated as a directed line, such that the two halves can be specified as the point sets that lie to the right of the directed line AB and the point set that lies to the right of the directed line BA. Computing the point sets in that manner will make things easier in the subsequent steps of the procedure. These two halves will serve as starting point (I swear pun not intended) to get the recursive procedure going, where they will be split into smaller and smaller point sets.

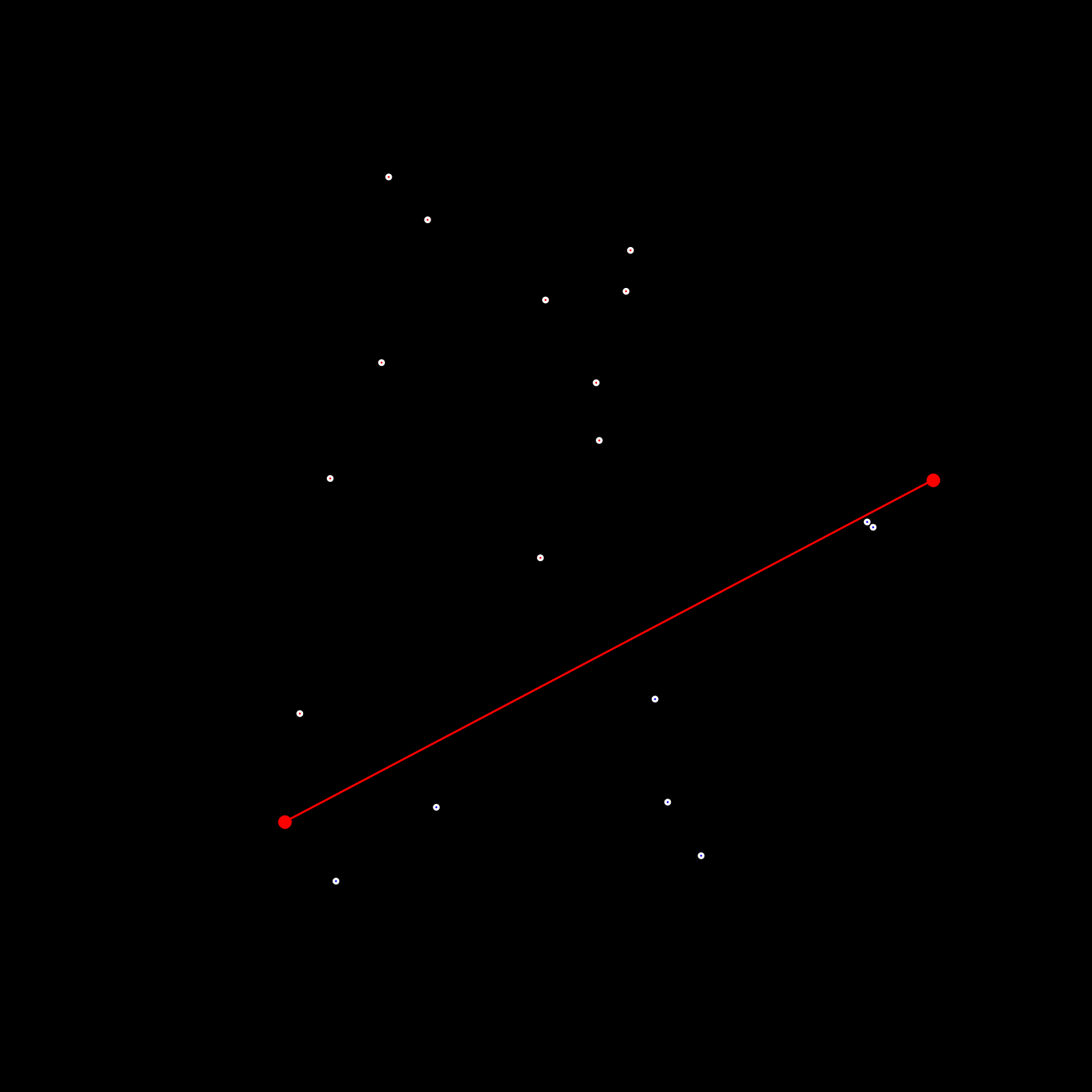
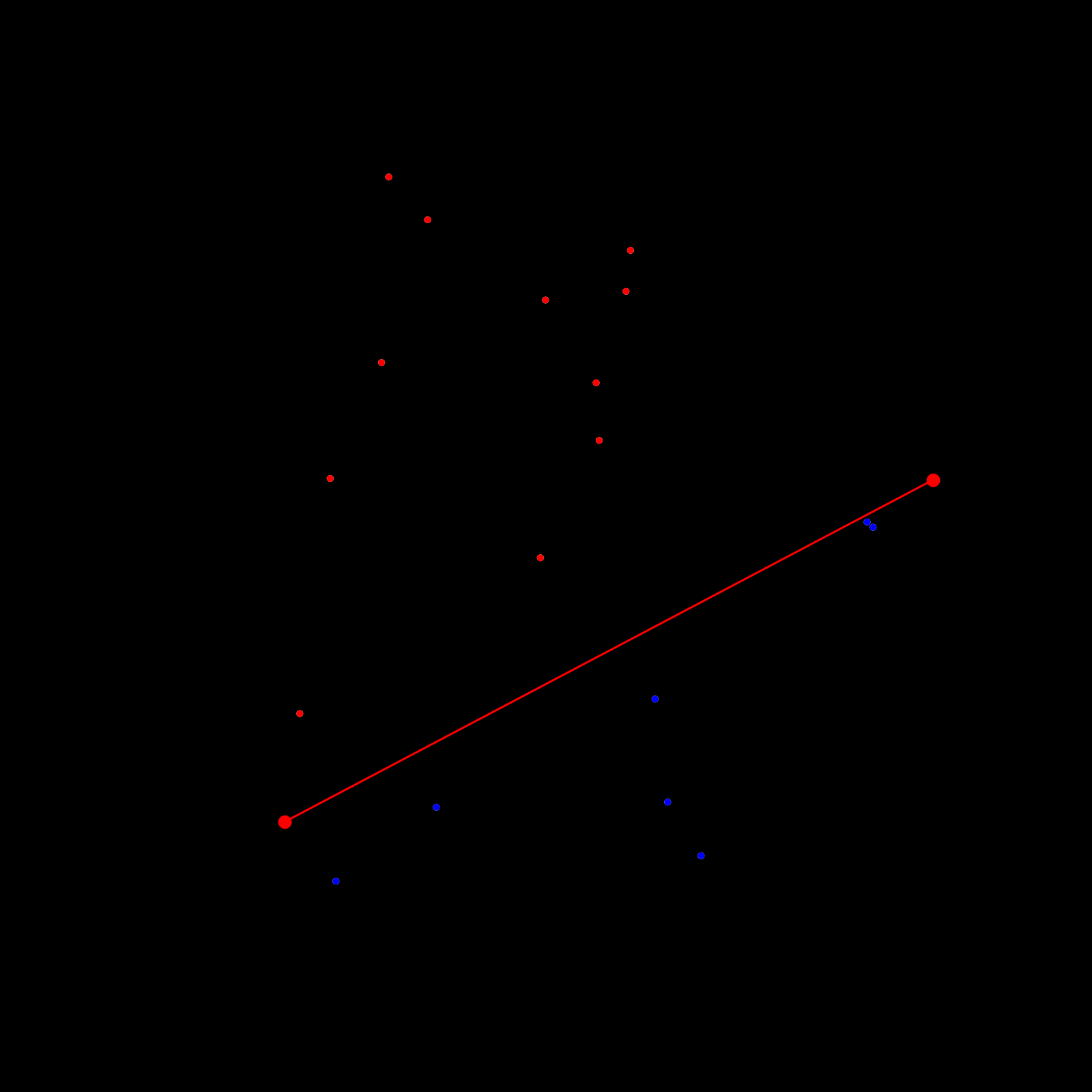
Starting out with the initial line and these two smaller point sets, the second function beings the recursive procedure:

1. Given a line (formed by two points that we'll call Q and P) as well as a set of points, where all the points in the set are positioned on one side of the line, we find the point that is furthest from this line. We call this point C.
2. This point lies on the extremity of the original set and is also essentially a vertex of the convex hull polygon.
3. With this new point we form a triangle with the two end points of the line. This triangle splits the given set of points into three subsets.
4. The set of points that falls inside of the triangle can be disregarded as none of these points could possibly be part of the convex hull.
5. The other two sets of points need to be processed recursively as they still contain points that belong to the convex hull. The first set being those points that fall on the right side of the directed line from point P to C and the other on the right side of the line going from C to Q.

Here's a visualization of this:

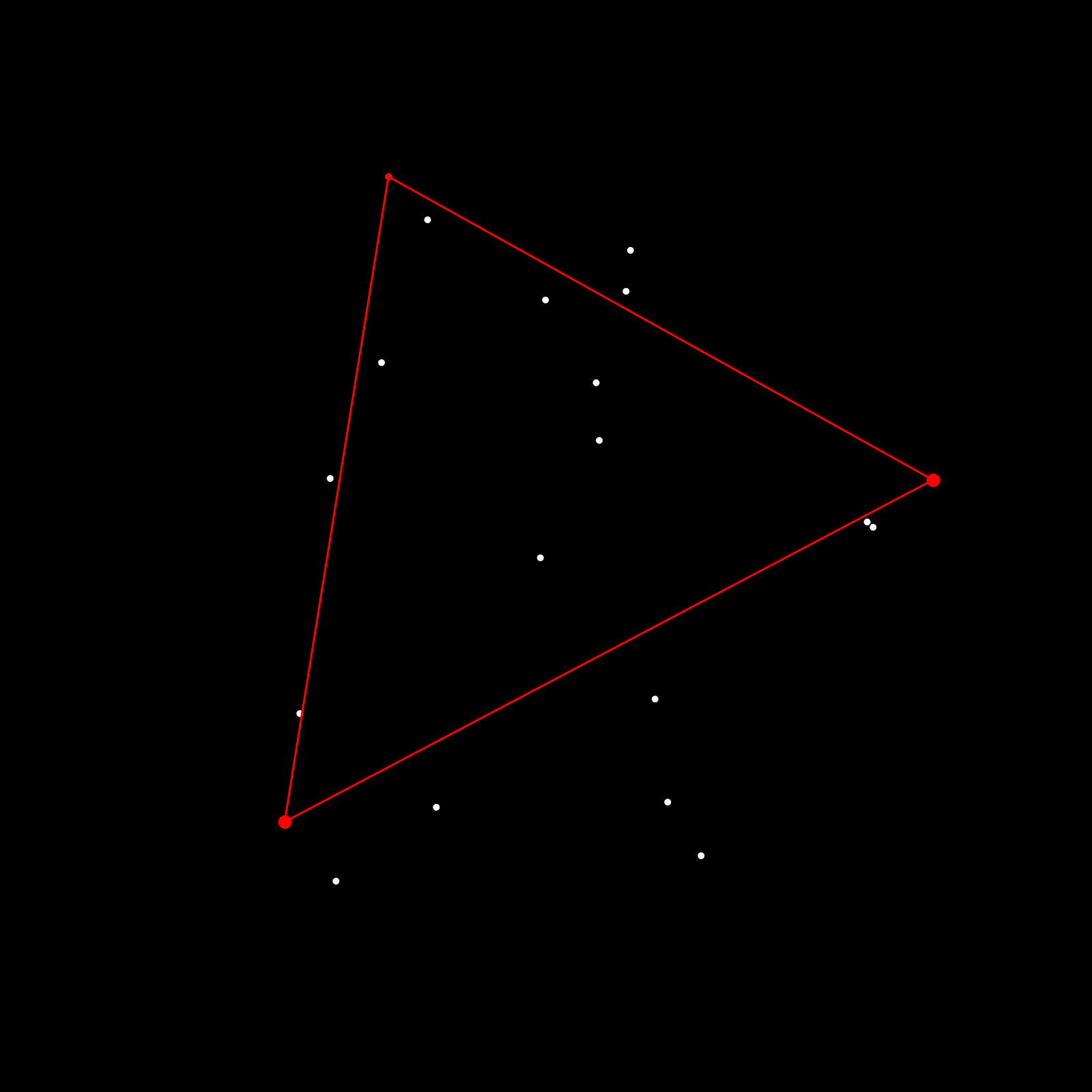
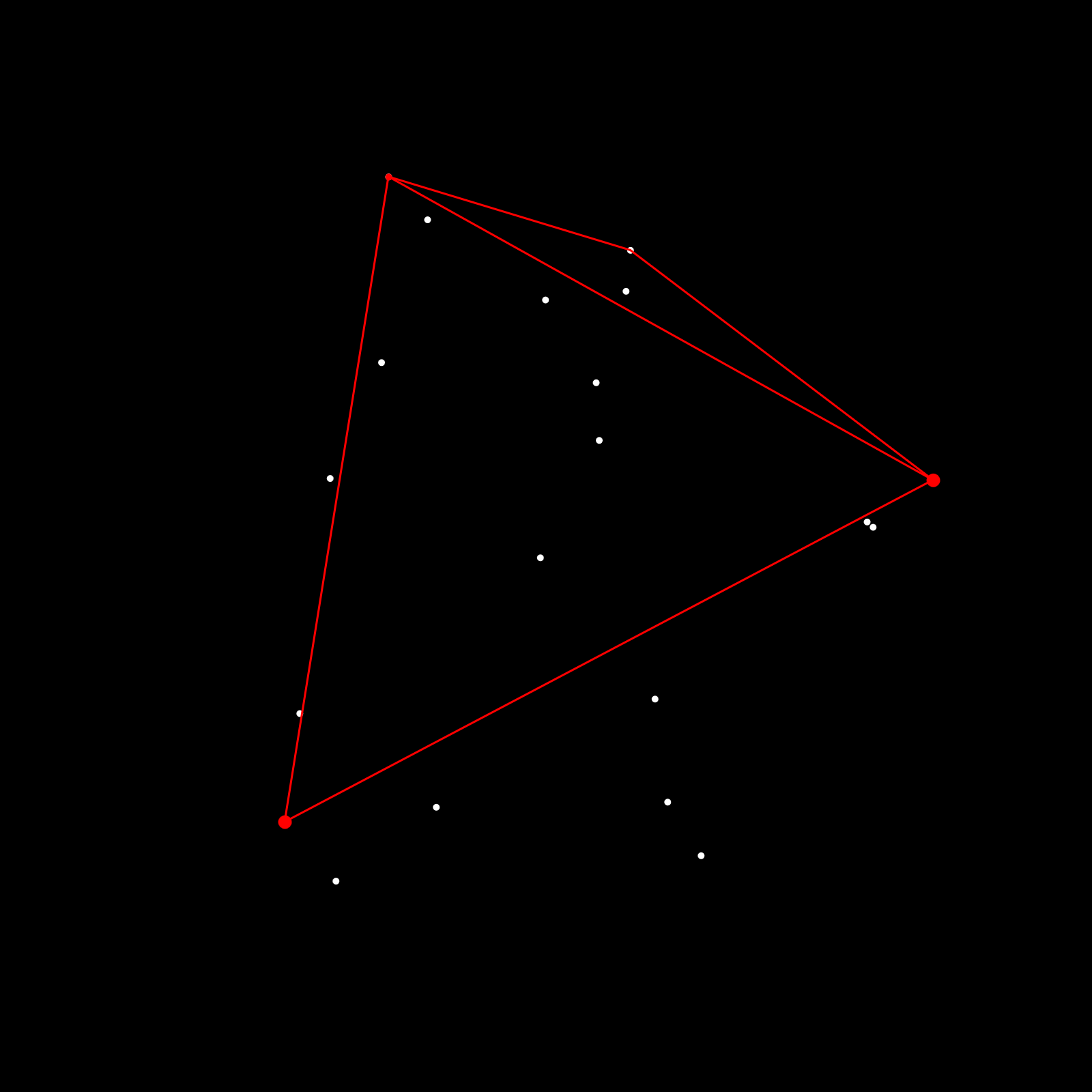
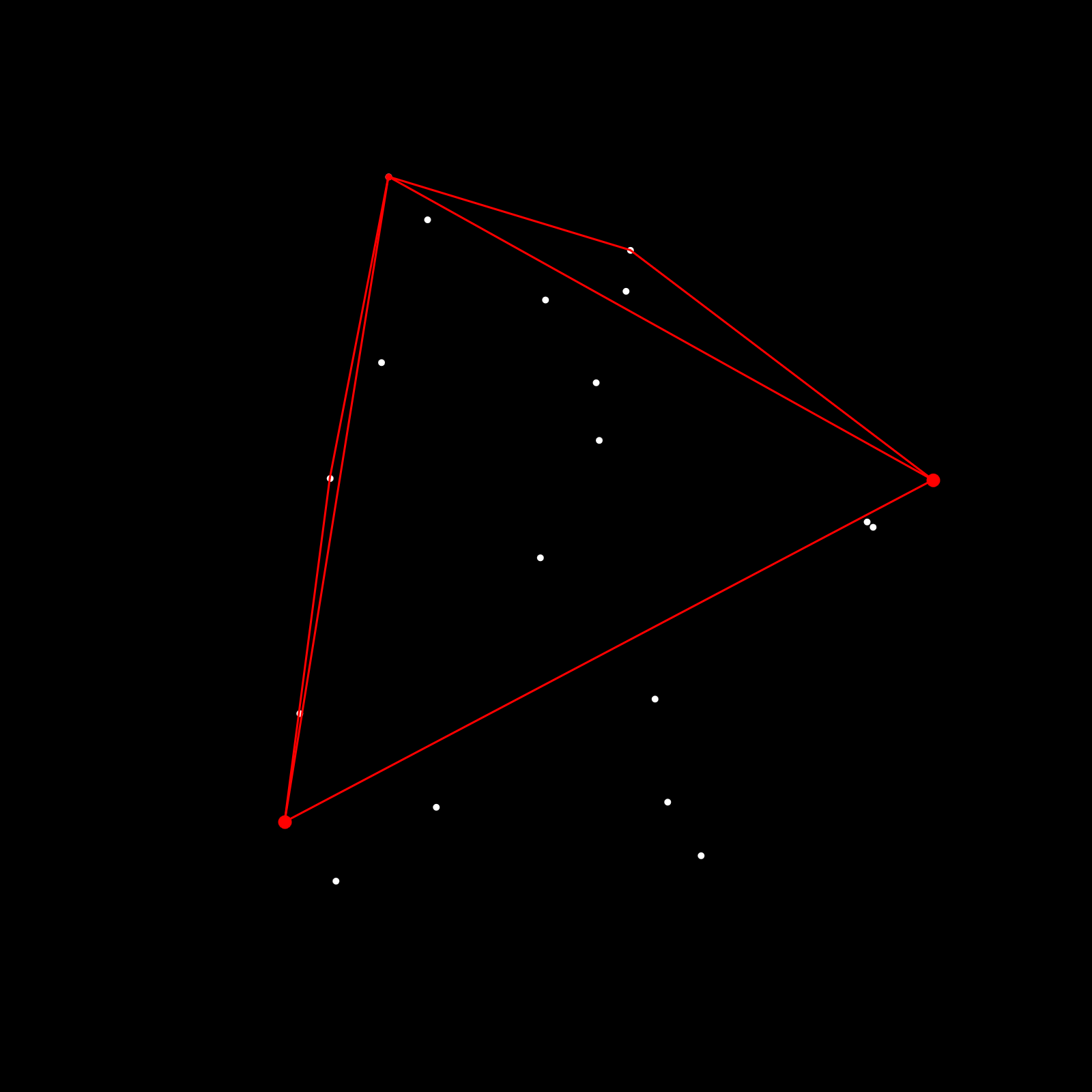
Essentially, starting a line, we find the furthest point towards that line, construct two new lines that connect that point with the endpoints of the previous line (forming a triangle). Then we repeat this procedure for the two new lines and the remaining points that fall outside of the triangle, until no points are left.

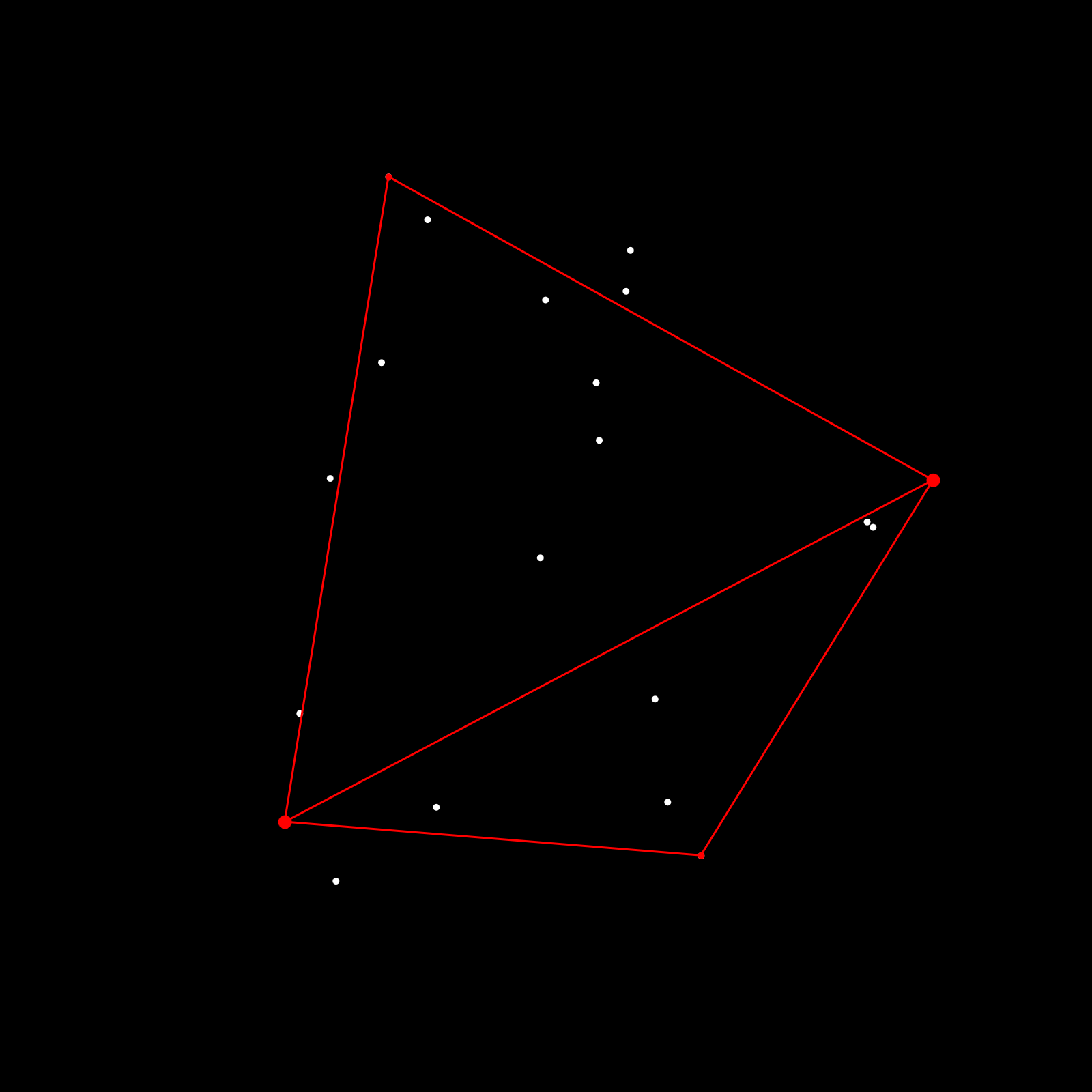
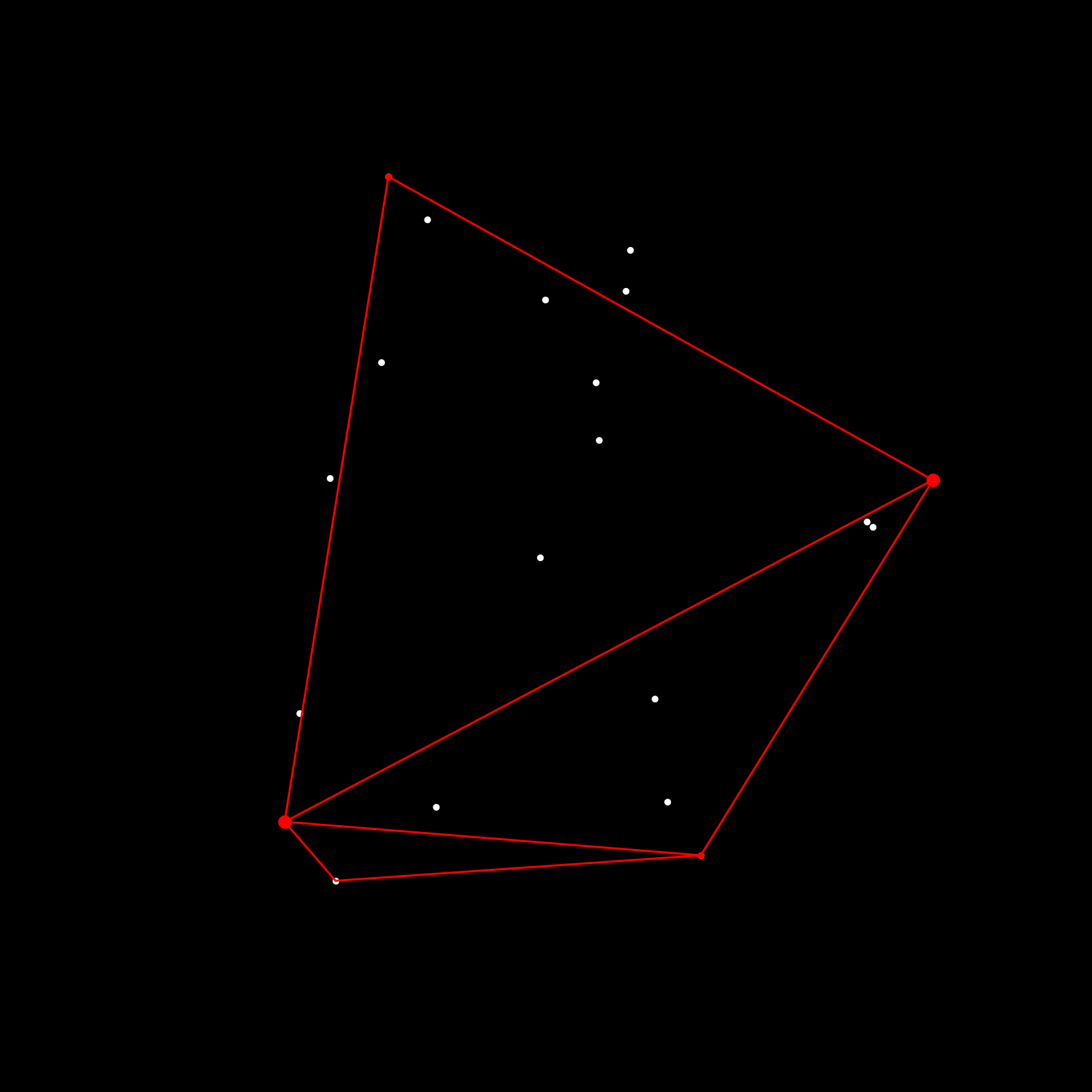
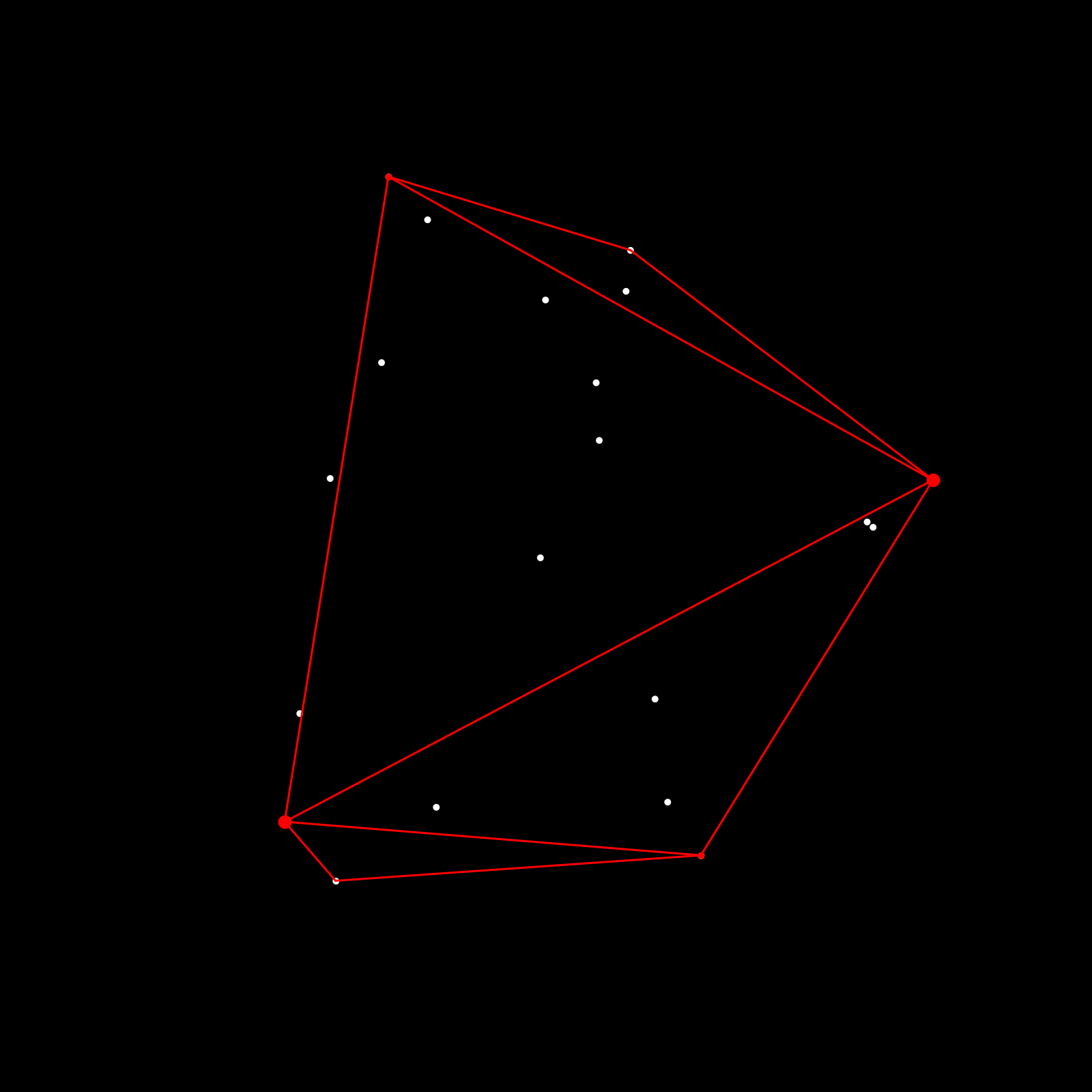
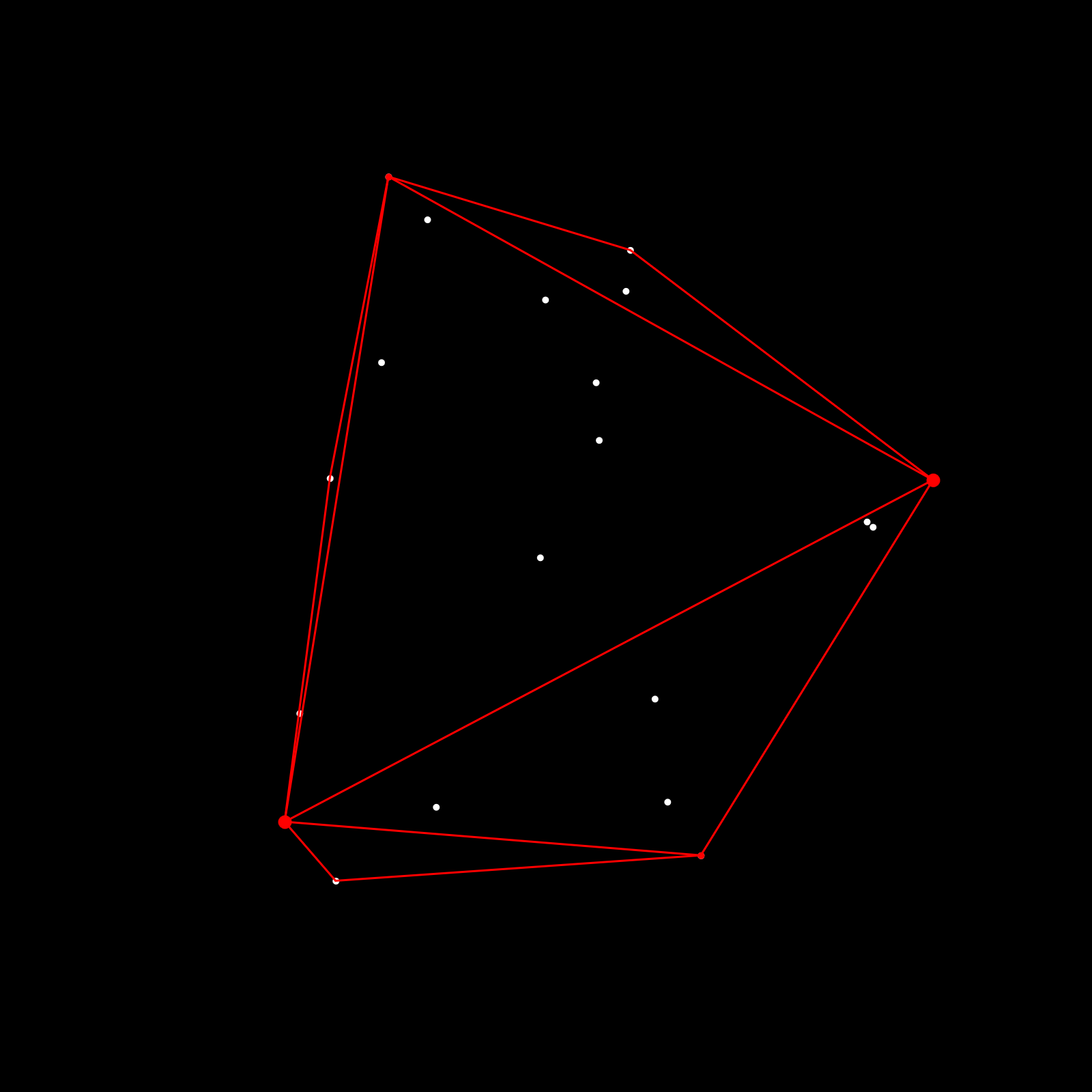
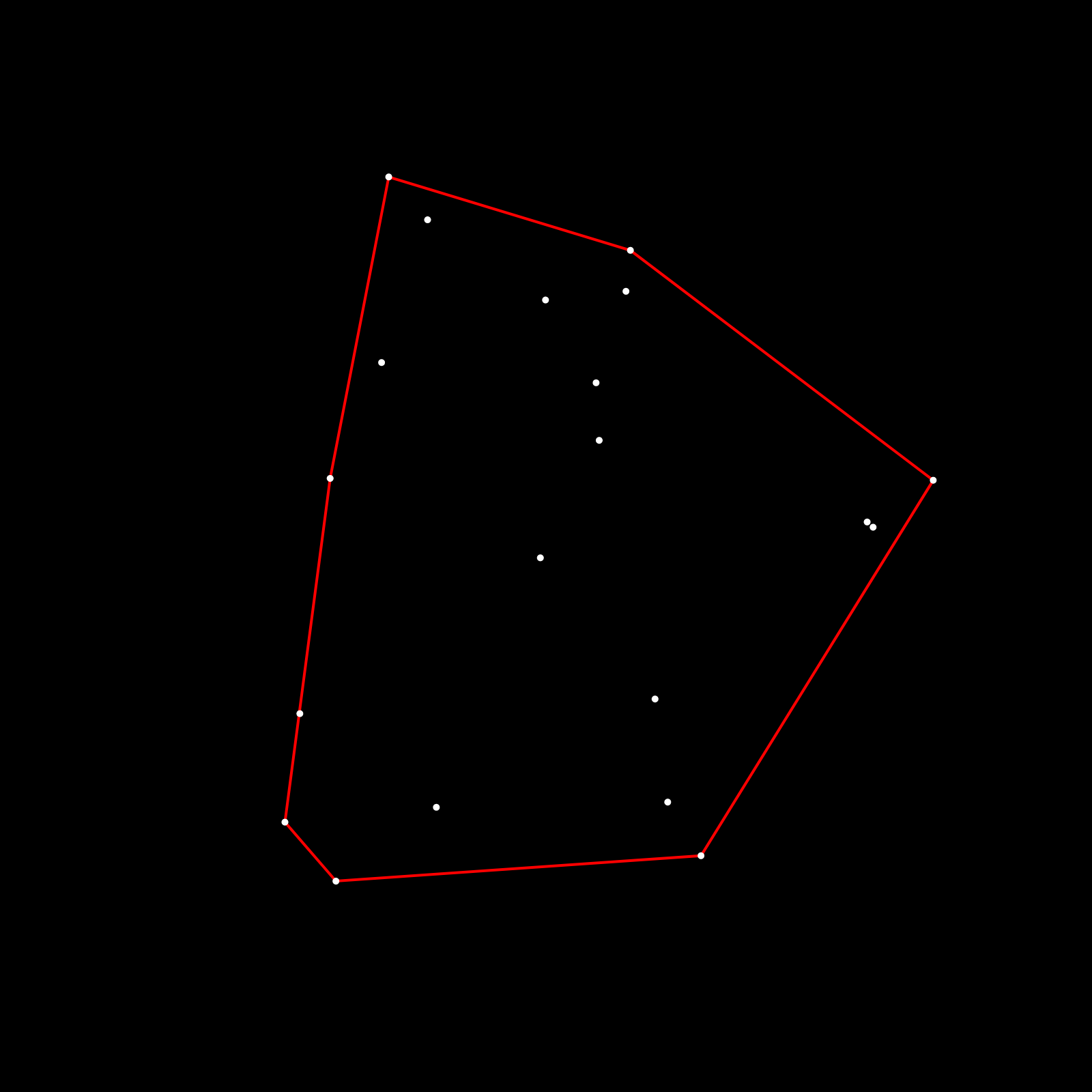
If recursion is new concept to you then that might be the hardest part of the process, here's a cool introduction:

Before we get to implementing the procedure however, let's first discuss some necessary helper functions.

Point Line Test

An important part of the procedure is determining on which side of the line the points fall, which is required to subsequently split the point set into two smaller halves. We'll do this in a separate subroutine.

There's a relatively simple formula for determining if a point is to the right or left of a line:

Where {x1, y1} and {x2, y2} are the coordinates of the end points of the line and {x, y} are the coordinates of the point that we are checking against. In code that would be:

// Source: https://stackoverflow.com/a/22668810/6688750
let d = (line.pt1.x - pt.x) * (line.pt2.y - pt.y) - (line.pt2.x - pt.x) * (line.pt1.y - pt.y)

This formula produces a number, where the sign of this number determines on which side of the line the point falls. If the number is positive the point falls on one side, if it is negative it falls on the other. If the value is zero then it means the point falls right on the line.

A good explanation for this point line test can be found here, including it as a screenshot as well:

Then a complete function to split a given set of points into two halves would be:

function splitPoints(pts, line) {
  // Empty arrays that we'll fill with the two halves
  let S1 = []
  let S2 = []
  
  // Check formula for given point
  for (let n = 0; n < pts.length; n++) {
    let pt = pts[n]

    let d = (line.pt1.x - pt.x) * (line.pt2.y - pt.y) - (line.pt2.x - pt.x) * (line.pt1.y - pt.y)

    if (d < 0) {
      S1.push(pt)
    } else if (d > 0) {
      S2.push(pt)
    }
  }

  // Return the two new sets
  return [S1, S2];
}

In this manner we return the two halves in an array for the subsequent steps.

Point Line Distance

Another important function here is determining the distance from a given point to the line. I didn't reinvent the wheel for this either and used the code from this SO answer, where we end up with the following functions:

function dist2(v, w) {
  return sq(v.x - w.x) + sq(v.y - w.y)
}

function distToSegment(p, v, w) {
  var l2 = dist2(v, w);

  if (l2 == 0) {
    return dist2(p, v);
  }

  var t = ((p.x - v.x) * (w.x - v.x) + (p.y - v.y) * (w.y - v.y)) / l2;

  t = max(0, min(1, t));

  return sqrt(dist2(p, {
    x: v.x + t * (w.x - v.x),
    y: v.y + t * (w.y - v.y)
  }));
}

function distancePointLine(pt, line) {
  return distToSegment(pt, line.pt1, line.pt2)
}

To find the furthest point from the line, we need to loop over all of the points in the given set:

function findFurthest(S, line) {
  let maxD = 0
  let idx = -1
  for (let n = 0; n < S.length; n++) {
    let d = distancePointLine(S[n], line)
    if (d > maxD) {
      maxD = d
      idx = n
    }
  }

  return idx
}

I think an important optimization that we can do here is combining this procedure and the previous one into one, such that we simultaneously halve the set and at the same time find the furthest points on both sides of the line. If you're a math whizz, and have ideas on how to do this, let me know. Alternatively, we could also use a data structure to not have to check all points and find the furthest one faster. Otherwise, I thought that it was adequately fast for my meager creative coding purposes.

Implementation

Now we can finally write the main code, and implement the entire procedure. To visualize things I'll be using the p5 library, which provides a couple of functions that make it very straightforward to draw shapes to the canvas, such as points, lines, polygons and also lets us color them with different colors.

Let's first setup a couple of things, like a procedure that can generate some random points to have our Quickhull algo run on:

let hullPts = []

let N_POINTS = 100 // number of points to be placed
let randomPoints = []

// create the canvas with p5 and make some random points 
function setup(){
  createCanvas(800, 800)
  randomPoints = placeRandomPoints(N_POINTS)
}

// samples N random points inside of a circle
function placeRandomPoints(N){
  let pts = []
  for(let n = 0; n < N; n++){
    let r = 300 * sqrt(random())
    let theta = random() * TAU

    let x = 400 + r * cos(theta)
    let y = 400 + r * sin(theta)

    pts.push({x: x, y: y})
  }
  return pts
}

With a little bit of trigonometry we uniformly sample random points inside of a circle that has a diameter slightly smaller than the overall canvas size. This method for sampling points is exemplified in this tweet by Yazid:

We also set up an empty array in which we will store the points that are part of the convex hull.

Now we can write the first function that creates the initial line from the horizontal extremes and creates the first split of the set:

function quickHull(){
  // sort the array by X coordinate
  randomPoints.sort(function(a, b){return a.x - b.x});

  // retrieve left-most and right-most points
  let leftMost = randomPoints[0]
  let rightMost = randomPoints[N_POINTS-1]

  // add points to the hull
  hullPts.push(leftMost)
  hullPts.push(rightMost)

  // create the directed lines 
  let splitLine1 = new makeLine(leftMost, rightMost)
  let splitLine2 = new makeLine(rightMost, leftMost)

  // compute the two halves
  let splits = splitPoints(randomPoints, splitLine1)

  // begin the recursive steps
  findHull(splits[0], splitLine1)
  findHull(splits[1], splitLine2)
}

// line object for convenience
function makeLine(pt1, pt2){
  this.pt1 = pt1
  this.pt2 = pt2
}

There's a bunch of things going on here already.

The most convenient method for finding the horizontal extremities of the set, is by sorting the points with their respective x coordinates. Then we can simply select the first and last element in that sorted array. We will add these to the empty array that holds the vertices of the convex hull polygon.

Next, we make use of a line object that we create for convenience purposes, and create, not one, but two lines. Remember, the direction of the line is important. Creating two separate lines, we can conveniently bake that direction in through the point order, which is simply reversed in the second line object.

To get the two halves of the point set, we will make use of the function that we discussed in the point line test section, which conveniently returns two new sets.

That being done, we're ready to start recursing! At the end of the initial function we invoke the second recursive function, which takes as input a line object and one of the two halves:

function findHull(S, line){
  // Check for an empty set of points
  if(S.length == 0){
    return 0 // base case terminates the function
  }else{
    // index of the furthest point from the line
    let idx = findFurthest(S, line)

    // add this point to the convex hull
    hullPts.push(S[idx])

    // create two new lines that form a triangle with the original line
    let triLine1 = new makeLine(line.pt1, S[idx])
    let triLine2 = new makeLine(S[idx], line.pt2)

	// create the new subsets 
	// made of the points that lie outside of the triangle
    let triSplit1 = splitPoints(S, triLine1)
    let triSplit2 = splitPoints(S, triLine2)

    // recurse on the two new sets
    findHull(triSplit1[0], triLine1)
    findHull(triSplit2[0], triLine2)
  }
}

The first thing that we need to do, to avoid an infinite recursion error, is to check for the base case where the set of points that is passed into the function is empty. In that case we simply terminate the function and invoke a return statement.

Otherwise there's a couple of things that we need to do. Firstly we'll have to find the point that is furthest from the line among the points in the given set, for this purpose we'll use the code that we discussed in the previous section. We can safely add this point to the array that holds the vertices of the convex hull.

We create two new lines that form a triangle with the given line, and then also compute the two new sets of points that fall outwards of this triangle. Finally we can make the recursive call where the function calls itself by invoking the findHull() function on those two new sets.

Lastly, because the Quickhull procedure doesn't return the polygon points in order, we require a final additional step that can achieve this. This is relatively straight-forward by virtue of dealing with a convex polygon. We'll simply sort the polygon vertices in clockwise order around the centroid by the respective angular value that they form with this centroid:

function sortPointsByAngle(pts){
  const center = pts.reduce((acc, { x, y }) => {
    acc.x += x / pts.length;
    acc.y += y / pts.length;
    return acc;
  }, { x: 0, y: 0 });

  // Add an angle property to each point using tan(angle) = y/x
  const angles = pts.map(({ x, y }) => {
    return { x, y, angle: Math.atan2(y - center.y, x - center.x) * 180 / Math.PI };
  });

  // Sort your points by angle
  const pointsSorted = angles.sort((a, b) => a.angle - b.angle);

  return pointsSorted
}

Another property of convex shapes is that their centroid always falls inside of it's boundaries, if our shape were concave on the other hand we would not be able to do this. Now we can simply draw this shape with the beginShape() and endShape() functions in p5.

Discussion and Concluding Thoughts

The quickhull is only one many methods for finding the convex hull. Other algos for the same purpose are the Graham Scan, Chan's Algorithm and the Gift-Wrapping Algorithm. Let me know if you want me to cover these as well in the future!

Hope you learned something new and enjoyed this post! If you did, you might also enjoy this post on the Bowyer-Watson algorithm and a less technical on Triangulations and the related Voronoi Diagrams:

Bowyer-Watson Algorithm for Delaunay Triangulation

The Bowyer-Watson algorithm for Delaunay triangulation is maybe one of the easier methods to implement and understand for obtaining a Delaunay Triangulation.

Gorilla SunAhmad Moussa

Delaunay Triangulation and Voronoi Diagrams

This is the first in a series of blog posts on Delaunay triangulation. This first part explains the task at hand and possible strategies to create a Delaunay Triangulation.

Gorilla SunAhmad Moussa

Otherwise, that's it for this one. Consider sharing this post on social media with frinds and family, it helps out a lot! And if you want come and say hi over on Twitter or leave a comment below! Cheers, happy coding!