Grids, in their various shapes and forms, have been an important backbone for my sketches since I started creative coding. I'd go as far as saying that grids are a prominent generative art archetype that sits at the foundation of many works. Two influential examples from an early generative art period would be Georg Nees' 1968 work Schotter (german word for Gravel) and Vera Molnár's 1974 artwork (Dés)Ordres (french word for (dis)order):

Grids go hand in hand with what computers do best: repetition. Grids are also by nature 'orderly'. We usually use grids and tables to neatly display information, align elements in an organized manner, as well as delimit text/numbers in such a way that it is easy for the eye to follow. However, observing these two artworks reveals a characteristic that is inherent to many generative pieces: the interplay between order and chaos. And I believe that that's one of the most fun aspects of gen-art, when you're presented with a new artwork for the first time and you have to figure out what the pattern is and where the twists and irregularities were introduced.
Here I'd like to conclude this little interlude and dedicate the rest of the post towards a grid-construction algorithm that I have used extensively in the past weeks. The algo is relatively straight-forward and unoptimized, but quite versatile. Here's a little index:



Grids and their Variations
Most of my first sketches were based on simple grids:

They allowed me to explore concepts like SDFs and noise fields (these two posts are also good starting points if you'd like to learn how to construct grids!). I have also experimented a bit with hexagonal grids and written about different strategies to construct them here. This leads to the next point that I'd like to discuss, that is irregular grids. When you google 'irregular grid' you get a bunch of odd looking grid layouts, some of them look like this:
Except for the first, each of these is an irregular grid in it's own right. Click on the thumbnail of each grid and it will take you to it's corresponding code in the openprocessing editor, I would however recommend to attempt recreating these by yourself first, since I found it to be an interesting little exercise.
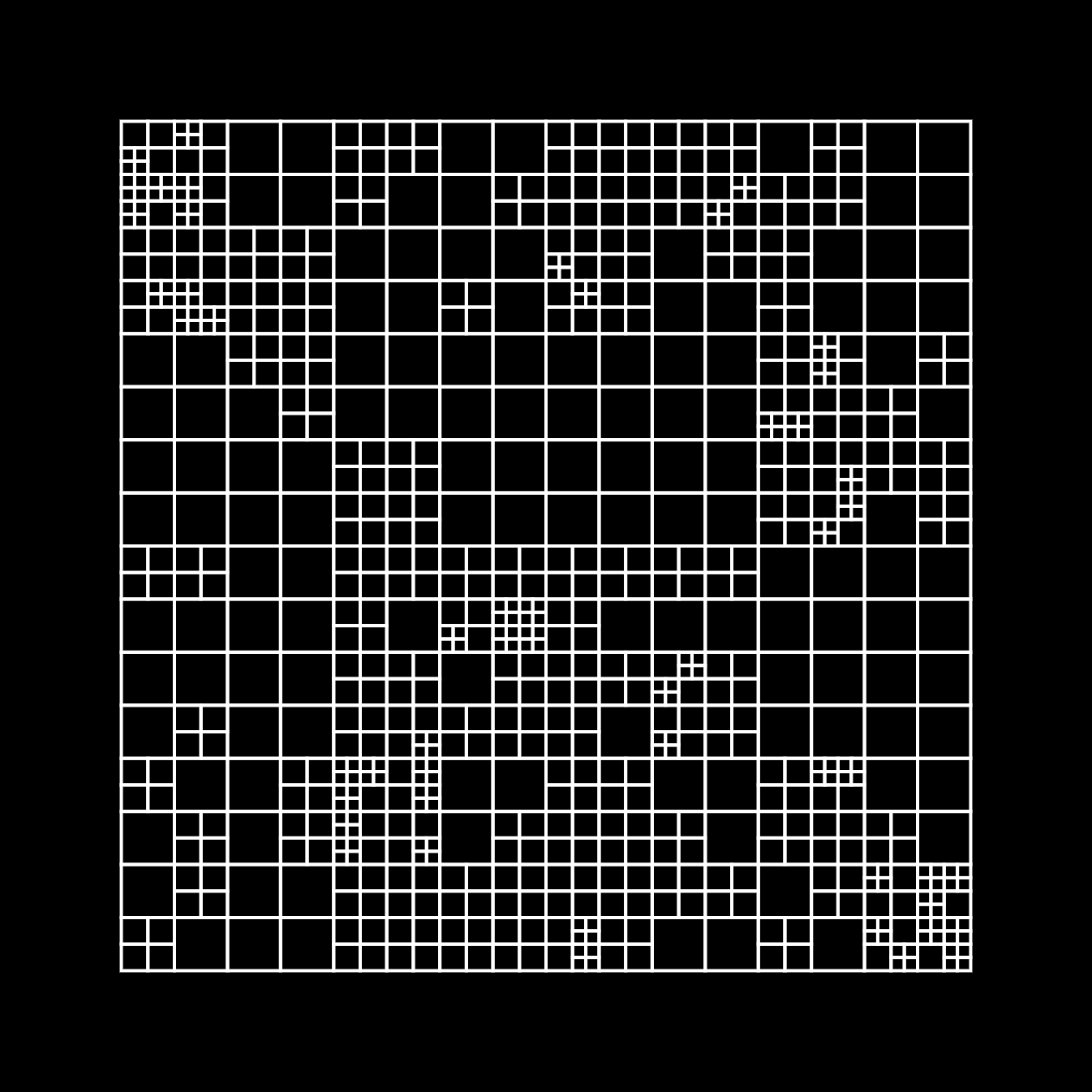
There is however one pattern that does not emerge in these grids, which occurred to me after reading a question by @griff420 on the birbsnest discord server:
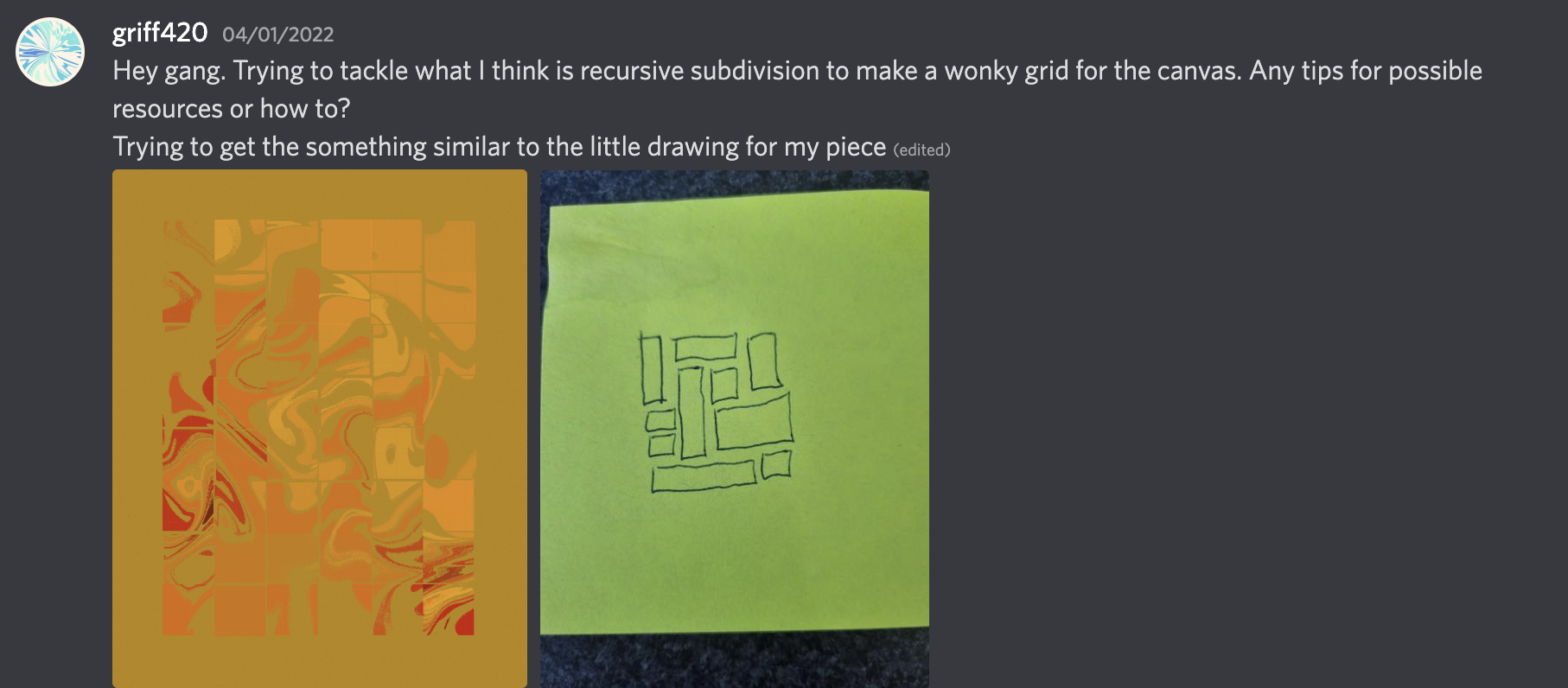
This is a bit tricky to explain, but it's not immediately evident how the rectangles could have been placed. In the middle we see three rectangles interlocking in a manner that wouldn't be possible to achieve by recursive subdivision.
Here is a nice article about a 'Recursive Mondrian' approach by Max Halford, who has an excellent blog btw. His approach is similar to the second and third grid examples I showed a little bit above. In such a grid it is clear where the larger rectangles were subdivided into smaller ones. However, you will never see rectangles protrude beyond the border of a larger containing rectangles. In the next section I'll give an intuitive explanation of an algorithm that can construct such an irregular grid.
A strategy for constructing an Irregular Grid
I came up with this strategy at the same time that I was working on my grid random walker code as well as the mini grand canyon sketch. What it has in common with them is that it is also based on an initial boolean grid, which we will use to do some pseudo rectangle packing. In this case, I am calling it 'pseudo' rectangle packing, because the size of the rectangles is chosen at runtime rather than being specified at a prior time.
Similar to the two previously mentioned sketches, we'll begin with a boolean grid, which basically consists of a 2D array of boolean values. Initially we'll set all of these values to true, which signifies that these spots are unoccupied. With the grid ready, we can begin placing some rectangles. We will go through the grid from the top left towards the bottom right, and depending how we arrange our loops we can do this in a row-wise or column-wise order.
First, we pick a reasonable rectangle size that spans a specific area of the grid. Here it's important to note that the sizes are relative, say we are working with a 12 by 12 grid and choose a rectangle size of 3x3, this would mean that the rectangle spans 3 columns and 3 rows. After having chosen a rectangle size, we will check if the grid at the current position, as well as the positions that the rectangle would span are unoccupied. If that is so, we can place the rectangle, and mark those spots in the grid as occupied.
We repeat this process while iterating over the grid. Once we are done and visualise the grid, we will notice that some unoccupied spots remain, this is due to choosing rectangle sizes that either overlapped with occupied spots in the grid or exceeded it's dimensions. Once we tackle the code we'll find that we have an implicit solution already. And this is pretty much all there is to it, we basically place some rectangles on a grid.
A Boolean Grid
Let's begin by creating the 2d boolean array! For starters we'll only consider the case where the shape of the grid is square (the final code will be able to produce any arbitrarily shaped grid however):
function setup(){
w = min(windowWidth, windowHeight);
createCanvas(w, w);
// size of the padding between grid and sketch borders
padding = w/12;
// number of rows and columns of the grid
gridDivsX = 15;
gridDivsY = 15;
// actual spacing between grid points
gridSpacingX = (w - padding*2)/gridDivsX;
gridSpacingY = (w - padding*2)/gridDivsY;
// here we populate the 2d boolean array
let bools = [];
for(let x = 0; x<gridDivsX; x++){
var column = [];
for(let y = 0; y<gridDivsY; y++){
column.push(1);
}
bools.push(column);
}
}Here gridDivsX and gridDivsY essentially specify the overall resolution of the grid and how many total empty spots it'll have. gridSpacingX and gridSpacingY are not used here yet, but we will need them when the time comes to draw our grid to the canvas, since they define the actual dimensions of the grid.
We also need to create an array in which we will store the positions of the rectangles that will make up the grid:
let rectInfo = [];
And that concludes the setup, now we can tackle the actual packing procedure.
The Packing Procedure
The packing procedure consists of a number of steps that I'll go over in this section. Our logic will be contained within a function called constructGrid():
function constructGrid(sizesArr){
for(let x = 0; x<gridDivsX-max(sizesArr)+1; x++){
for(let y = 0; y<gridDivsY-max(sizesArr)+1; y++){
}
}
}There's already a bunch of things going on here. The main part of the function consists of a nested loop that goes over the grid. The function also requires an input called sizesArr, which basically is an array from which we will draw different sizes at random. We will use these sizes to create and place randomly sizes rectangles on the grid.
In the loop condition we also don't loop over the entire grid, for now we ignore the spots where rectangles could potentially exceed the dimensions of the grid and throw an error. The next step now is coding the rectangle placing logic.
So, at this point, since we haven't chosen dimensions for the rectangle that is to be placed, and until proven otherwise, we can make the assumption that the rectangle should theoretically fit, whatever size it may have. We designate this fact with a boolean variable:
var fits = true;Now we can actually choose dimensions for our rectangle. At random, we select different sizes for the rectangle's width and height from our sizes array:
xdim = random(sizesArr);
ydim = random(sizesArr);
As mentioned earlier there are two conditions during which the rectangle does not fit: it either exceeds the bounds of the grid, or it overlaps with another rectangle that we already placed. We can check if it is within bounds:
if(x + xdim > gridDivsX || y + ydim > gridDivsY){
fits = false
}And check if it overlaps with another rectangle:
for(let xc = x; xc < x + xdim; xc++){
for(let yc = y; yc < y + ydim; yc++){
if(bools[xc][yc] == 0){
fits = false
}
}
}Now if both of these checks fail and 'fits' remains true, it is safe to place the rectangle. In this case we need to mark the area that the rectangle will occupy as occupied and save the rectangle's position and dimensions for later use since we are not going to draw it immediately:
if(fits){
// mark area as occupied
for(let xc = x; xc < x + xdim; xc++){
for(let yc = y; yc < y + ydim; yc++){
bools[xc][yc] = false
}
}
rectInfo.push(new makeRect(x,y,xdim,ydim))
}
You probably noticed that we are storing the rectangle information as a custom object, which is useful if we want to store additional information with each rectangle, but is not necessary. The class in this case is quite minimal and looks something like the following:
function makeRect(posX, posY, dimX, dimY){
this.posX = posX;
this.posY = posY;
this.dimX = dimX;
this.dimY = dimY;
// other stuff here
}
Visualising the Grid
Drawing the grid to the canvas now is relatively straight forward, we simply loop over the array in which we stored our rectangle information:
function drawGrid(){
for(let n = 0; nHere's where the gridSpacingX and gridSpacingY variables we computed at the start come into play. We need to multiply the rectangles' position and dimensions with the actual dimensions of our grid to get accurate sizes. I really like this approach, because in this manner we can stretch the grid horizontally and vertically with fairly little effort. Let's first put together everything we have discussed so far:
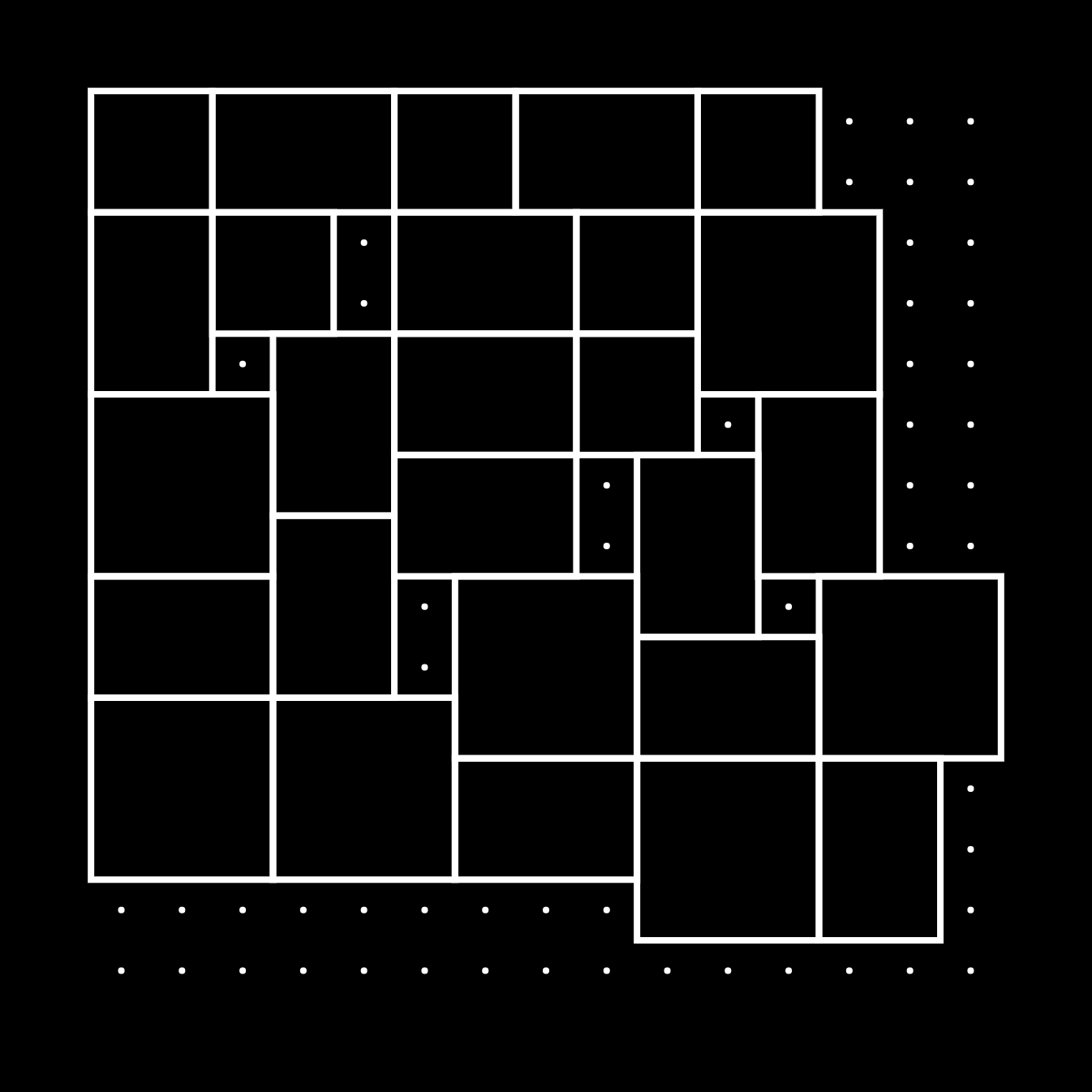
Notice here that our strategy wasn't able to completely fill out the entire grid, and there were some empty spots left over. These spots are marked with dots. However before we tackle filling out these spots, let make this grid adjustable to different canvas sizes!
This change can be effectuated by introducing a couple more variables in the setup function:
function setup(){
// for demonstration purposes
randomSeed(0);
widMod = 1 // width modifier
lenMod = 1 // height modifier
w = min(windowWidth, windowHeight);
wx = w*widMod
wy = w*lenMod
createCanvas(wx, wy);
// size of the padding between grid and sketch borders
padding = w/12;
// number of rows and columns of the grid
gridDivsX = 15;
gridDivsY = 15;
// actual spacing between grid points
gridSpacingX = (wx - padding*2)/gridDivsX;
gridSpacingY = (wy - padding*2)/gridDivsY;
// rest is kept the same as before
}
Now we can control the aspect ratio of the sketch simply by specifying it with the widMod and lenMod variables. For demonstration purposes I am using a fixed seed number:
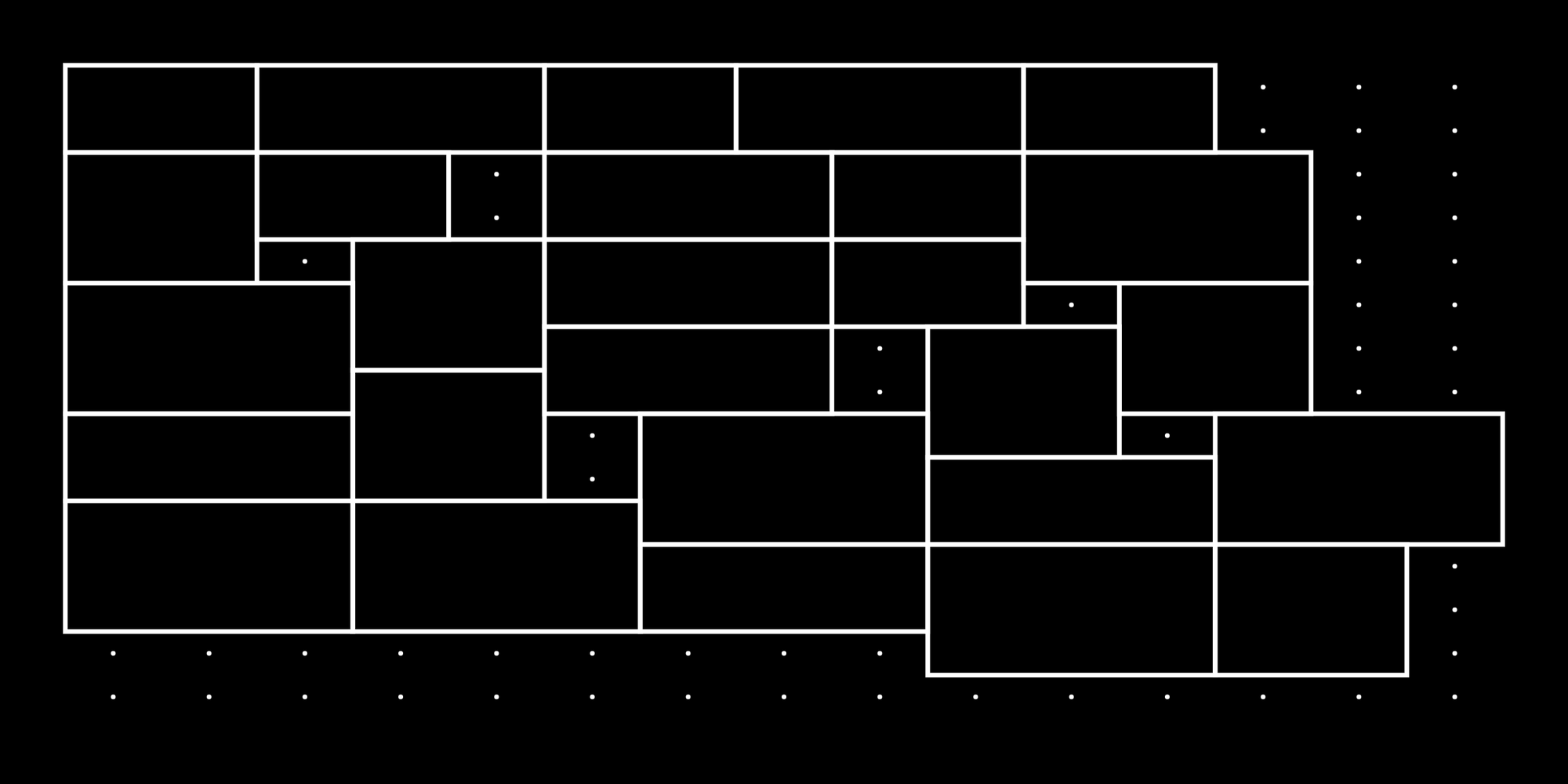
If you're not a fan of the stretched out look, we can also multiply the grid divisions by the width and length mods to obtain a consistent look:
gridDivsX = 15*widMod;
gridDivsY = 15*lenMod;
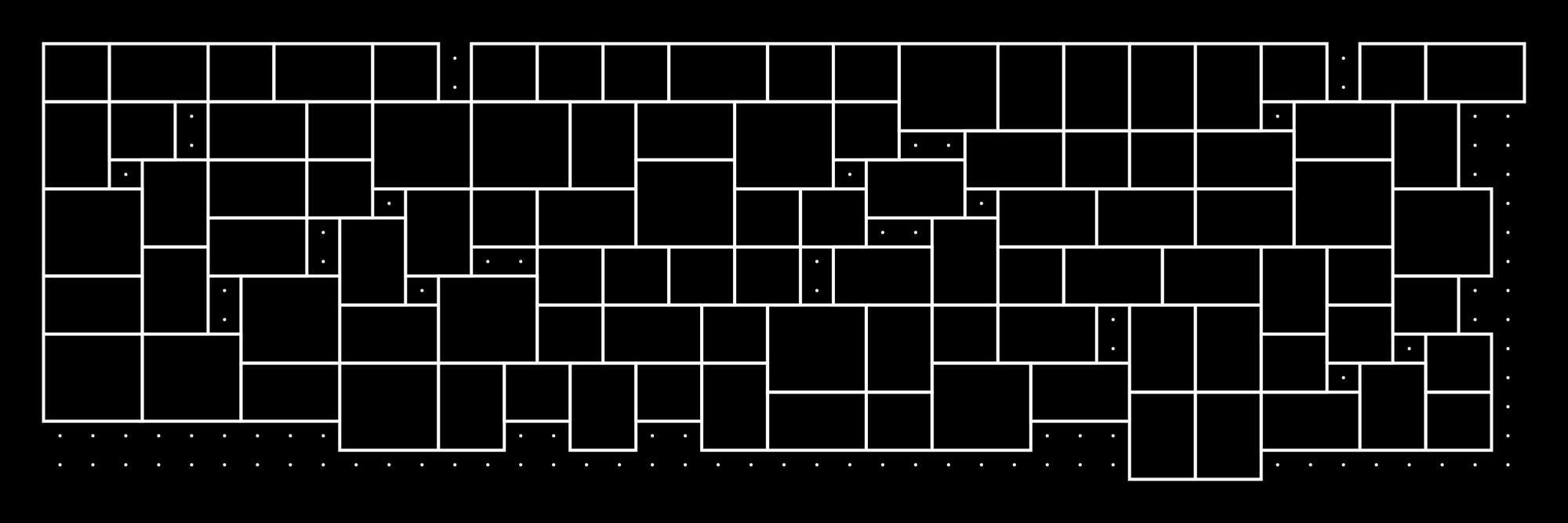
That should give you a couple of options to obtain a variety of sketches that don't always have a square aspect ratio!
Filling out the Leftover Gaps
Now on to completely filling out the grid! For this we simply need to make an additional constructGrid() call:
constructIrregularGrid([2,3]);
constructIrregularGrid([1]);
And we obtain a grid that looks something like this:
This works because on the subsequent constructGrid() call we are going over the same boolean grid, the spots that have already been marked as occupied will, well, still be occupied, but we get a chance to fill out those spots that are still free. And since we pass an array that only has one size the rectangles will inevitably fill a single grid cell. Now you don't necessarily need to fill it out this way and can pass in different grid sizes.
Different grid styles
We can exploit this behaviour and obtain completely different grid styles! Let's make a little modification that allows us to control the rectangle widths and heights independently:
function constructIrregularGrid(sizesArrX, sizesArrY){
for(let x = 0; xNow we are passing in two independent arrays, one that specifies the range of widths that rectangles can have, and another one for their heights. You can obtain a variety of different grids in this manner:



And that's pretty much everything that goes into this algorithm, if I stumble across any additional modifications I will make sure to include them here. If you do end up using this, and/or make anything with please @ me on Twitter when you share it!